Flows
For a flow, the vector field Φ(x) is a linear function of the position in the phase space, that is,The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior.
Geometrical definition
A dynamical system is the tuple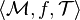 , with
, with 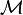 a manifold (locally a Banach space or Euclidean space),
a manifold (locally a Banach space or Euclidean space),  the domain for time (non-negative reals, the integers, ...) and f an evolution rule t→f t (with
the domain for time (non-negative reals, the integers, ...) and f an evolution rule t→f t (with  ) such that f t is a diffeomorphism of the manifold to itself. So, f is a mapping of the time-domain
) such that f t is a diffeomorphism of the manifold to itself. So, f is a mapping of the time-domain  into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain
into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain  .
.Measure theoretical definition
 is said to be Σ-measurable if and only if, for every
is said to be Σ-measurable if and only if, for every  , one has
, one has  . A map τ is said to preserve the measure if and only if, for every
. A map τ is said to preserve the measure if and only if, for every  , one has μ(τ − 1σ) = μ(σ). Combining the above, a map τ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple (X,Σ,μ,τ), for such a τ, is then defined to be a dynamical system.
, one has μ(τ − 1σ) = μ(σ). Combining the above, a map τ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple (X,Σ,μ,τ), for such a τ, is then defined to be a dynamical system.The map τ embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates
 for integer n are studied. For continuous dynamical systems, the map τ is understood to be finite time evolution map and the construction is more complicated.
for integer n are studied. For continuous dynamical systems, the map τ is understood to be finite time evolution map and the construction is more complicated.
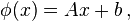


 .
. .
. of a quaternion behaves like a vector
of a quaternion behaves like a vector  in three dimension vector space, and the real part a behaves like a scalar in
in three dimension vector space, and the real part a behaves like a scalar in  . When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector:
. When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector:  .
. , where:
, where: is vector multiplication,
is vector multiplication, is vector cross product (a vector),
is vector cross product (a vector), is vector scalar product (a number).
is vector scalar product (a number). .
. , as can be verified by direct calculation.
, as can be verified by direct calculation.
