Quaternions and spatial rotation

Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may be more efficient. Quaternions have found their way into applications in computer graphics, robotics, navigation, molecular dynamics and orbital mechanics of satellites.

The complex numbers can be defined by introducing an abstract symbol i which satisfies the usual rules of algebra and additionally the rule i² = −1. This is sufficient to reproduce all of the rules of complex number arithmetic: for example, .
In the same way the quaternions can be defined by introducing abstract symbols i, j, k which satisfy the rules i² = j² = k² = ijk = −1 and the usual algebraic rules except the commutative law of multiplication (a familiar example of such a noncommutative multiplication is matrix multiplication). From this all of the rules of quaternion arithmetic follow: for example, one can show that .
The imaginary part of a quaternion behaves like a vector in three dimension vector space, and the real part a behaves like a scalar in 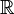. When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector: .
Those who have studied vectors at school might find strange to add a number to a vector, as they are objects of very different natures, or to multiply two vectors together, as this operation is usually undefined. However, if one remembers that it is a mere notation for the real and imaginary parts of a quaternion, it becomes more legitimate.
We can express quaternion multiplication in the modern language of vector cross and dot products (which were actually inspired by the quaternions in the first place). In place of the rules i² = j² = k² = ijk = −1 we have the vector multiplication rule , where:

• is vector multiplication,
• is vector cross product (a vector),
• is vector scalar product (a number).

Vector multiplication is noncommutative (because of the cross product), while scalar-scalar and scalar-vector multiplications commute. From these rules it follows immediately that .
The (left and right) multiplicative inverse of a nonzero quaternion is , as can be verified by direct calculation.